:: Final Movie

::Final Rendering

I conducted various experiments for rendering.

::Final_Shot

::Final_Making 3D Printing

I make a 3D Printing model by 3D Print. I had a quite a time making it. Because This Supporter must be removed. This print(uPrint) features a soluble support removal system, allowing for hands-free removal of the model support material.(http://www.youtube.com/watch?v=VYTN_xAe_-M)

::Experiment_Making 3D Model_02

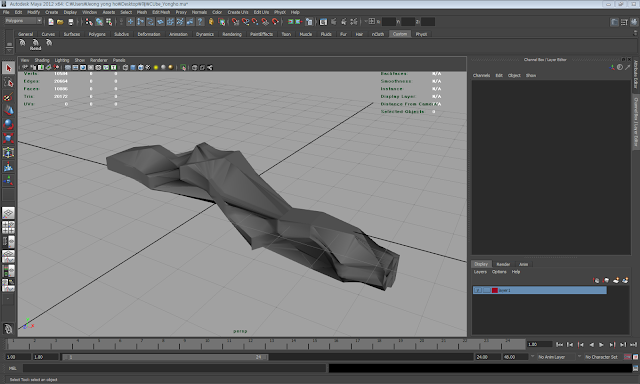
::Experiment_Making 3D Model_01

I aligned the 11 planar figure in straight rows. And I tried to connect it. So I was able to making a 3D model. But there's a problem with the plane interacts the others. 

So I wrapped mesh surface around this. I finally solved the problem.

::Experiment_Development Planar Figure

We live in a 3 dimensional world but we constantly want to represent what we see in 3D in two dimensions. I wanted to converting from 3d to 2d. So I try to find a more suitable way.

I have learned about the planar figure. I think it's a good method. So I make 11 planar figure.  

--------------------------------------------------------------------------------------------------------------------------------------------
Theory

The Cube

A tree is a connected graph with n nodes and n - 1 edges. Figure 1 shows the six six-node trees [2]. We may arrange the six nodes of a tree into three pairs and specify that the members of a pair may not be adjacent. Let us call such a tree a “paired tree”. Thus, a paired tree is a tree together with a perfect matching in its complement.

Figure 1. The six six-node trees.

There are eleven distinct pairings of the six-node trees. There are also eleven unfolded cubes. There is a one-to-one mapping from the set of unfolded cubes to the set of paired six-node trees. The mapping is shown in Figure 2.

Figure 2. Mapping between unfolded cubes and paired six-node trees.

There is a simple procedure for finding the unique paired tree that an unfolded cube maps to.

1. Pair the squares of an unfolded cube if the squares become opposite faces on folding. A cube has three pairs of opposite faces.
2. Replace the squares with points.
3. Connect two points if the squares they replaced were adjacent.

An example is shown in Figure 3.

Figure 3. Procedure for mapping an unfolded cube to a paired tree.

This procedure will always produce a tree because the six squares of an unfolded cube will always be connected along five lines. If there were fewer than five connections, the six squares would not all be joined into a unit. If there were more than five connections, the unfolded cube could not lie on a plane. For similar reasons, a six-node tree must have five edges. If a six-node graph has less than five edges, the six nodes will not all be joined into a unit. If a six-node graph has more than five edges, there will be a cycle in it.

This procedure will never pair adjacent nodes in a tree because opposite faces of a cube are never adjacent. No unfolding of a cube can make opposite squares adjacent

Finally, it is clear that this procedure will always produce a unique paired tree. An unfolded cube maps to only one tree and uniquely describes the pairing of the nodes of the tree.

--------------------------------------------------------------------------------------------------------------------------------------------

I make a regular hexahedron and draw a planar figure representing a cube cut open and laid flat. 


                                                                                                                                                    A planar figure_01

                                                                                                                                                    A planar figure_01